Análise de algoritmos

Introdução à análise de algoritmos¶

Um algoritmo pode ser definido como uma sequência de passos usada para resolver algum problema. Naturalmente, em computação, estamos mais interessados em problemas que possam ser abstraídos usando matemática e algoritmos para esses problemas que sejam precisos na definição de cada passo e passíveis de reprodução por um computador (ou modelo de computação). Sendo assim, podemos estabelecer a seguinte relação entre o que é prático e o que é abstrato no estudo da resolução de problemas:

• Programa ~ Linguagem de programação
• Computador físico ~ Algoritmo
• Pseudocódigo ~ Computador abstrato (ou modelo de computação)

Nosso objetivo é estudar algoritmos do ponto de vista abstrato (segunda coluna acima). A primeira etapa, portanto, é formalizar bem um problema para que não se tenha dúvidas com relação ao que é dado como entrada e o que se espera como resultado (saída). Por exemplo, o problema de ordenar um conjunto de números inteiros em um arranjo pode ser formalizado da seguinte forma:

• Entrada: sequência de números inteiros organizados em um arranjo $a = [a_1 , a_2 , \cdots , a_n ]$
• Saída: permutação Θ $[a_1^\Theta , \cdots ,a_n^\Theta ]$ tal que $a_1^\Theta \leq a_2^\Theta \leq \cdots \leq a_n^\Theta$

Modelo de computação e conceitos de análise¶

O primeiro requisito ao se trabalhar com algoritmos é ser capaz de analisá-los, isto é, precisamos ser capazes de determinar certas características do algoritmo antes mesmo de implementá-lo e executá-lo na prática. Por exemplo, é muito comum que estejamos interessados em algoritmos eficientes. Precisamos, portanto, estabelecer como será o computador abstrato ao qual o algoritmo estudado se refere. No estudo de algoritmos vamos adotar um modelo de computação abstrata que reflete características muito comuns de arquiteturas computacionais contemporâneas: o modelo RAM – Random Access Machine. As seguintes características estão presentes em algoritmos projetados para o modelo RAM:

• As instruções dos algoritmos são executadas sempre sequencialmente, sem nenhum tipo de con- corrência ou paralelismo;
• Vamos assumir que os dados manipulados pelos algoritmos são organizados em uma memória de acesso aleatório e organizada em palavras;
• Tipos de dados: inteiros, ponto flutuante, arranjos de palavras (sequência de inteiros ou ponto flutuante), qualquer outra estrutura de dados derivada;
• Operações aritméticas em geral: +, −, ÷, ×, % , etc.;
• Controle: while, for, do .. while, return, subrotinas/funções, condicionais (if, else), operadores de comparação (==, <, >, etc.);
• Atribuições de variáveis são representadas como =.

Pseudocódigo no modelo RAM.¶

Vamos ver um exemplo de algoritmo para o problema de contar quantas vezes um número inteiro n ocorre em um arranjo de inteiros v. Formalmente, entrada: inteiro n e arranjo de inteiros v; saída: inteiro c representando o número de ocorrências de n em v. O tamanho de v é representado nesse exemplo como |v|:

conta-ocorrencias(n, v)
c = 0
for i = 1 to |v|
  if v[i] == n
    c = c+1
return c

Dimensões de análise¶

Diferentes instâncias podem demandar diferentes níveis de dificuldade para a execução do algoritmo. Esperamos que, seja em uma máquina abstrata ou não, cada problema é passível de encontrar instâncias fáceis (entradas fáceis) ou instâncias mais difíceis (entradas mais difíceis). Por exemplo, para o problema de contar as ocorrências de um número no arranjo não é razoável assumir que o mesmo algoritmo irá se comportar da mesma forma para um arranjo de 10 elementos em comparação a um arranjo de 107 elementos. Por esse motivo, vamos sempre estudar algoritmos em função do tamanho da entrada que lhe é apresentada. Com isso, temos nosso principal objetivo em análise de algoritmos: para um algoritmo, determinar seu consumo de tempo e/ou espaço frente a instâncias cada vez maiores na entrada.

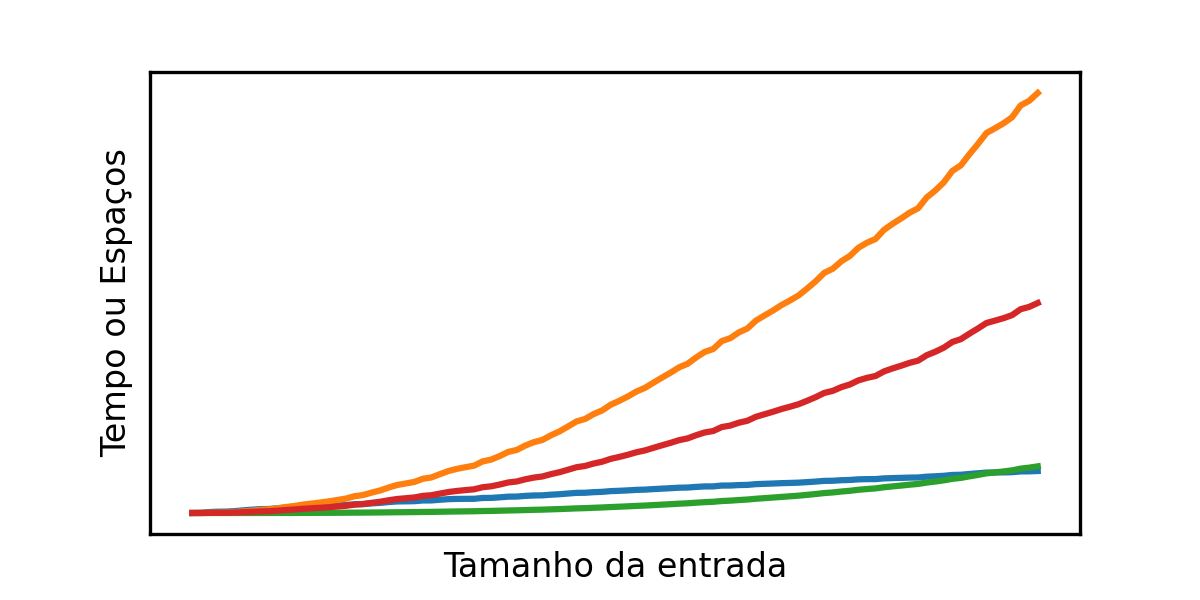
As duas noções de dificuldade para um computador abstrato que estamos interessados são:

1. Tempo: quantas operações básicas um algoritmo executa para uma dada instância do problema. Nesse caso, ao invés de medir tempo de relógio, nós vamos contar quantas operações um algoritmo executa.
2. Espaço: quanto de espaço (palavras do RAM) além da entrada o algoritmo utiliza em função também do tamanho da instância de entrada.

Chamamos portanto de operação básica aquilo que pretendemos medir em um algoritmo. Na prática, poderíamos medir tanto operações específicas quanto conjuntos de operações de interesse. Para facilitar a discussão, iremos focar em análises que consideram apenas uma operação básica como alvo de estudo. Essa escolha é feita por quem analisa o algoritmo, mas por exemplo: (a) para um problema de ordenar números em um arranjo pode ser natural pensar que as operações que são mais importantes para determinar a ordem entre os elementos são as operações que comparam dois elementos do arranjo: $a[i] ≤ a[ j]$, por exemplo; (b) para um problema matemático de encontrar o máximo divisor comum entre dois números pode ser uma boa prática escolher operações aritméticas (possivelmente o resto da divisão, pensando na estratégia de Euler) como operação básica. Portanto, não existe regra mas existem boas práticas.

Contexto de análise¶

O pior caso representa instâncias para o problema que fazem o algoritmo trabalhar ao máximo: usar o máximo de espaço ou executar o máximo de operações básicas possível. O melhor caso é o contrário, indicando cenários otimistas para o algoritmo. Finalmente, o caso médio representa os casos em que o algoritmo trabalha de acordo com esperado na média, para isso sendo necessário assumir algumas características da entrada (por exemplo, independência e instâncias de entrada igualmente prováveis).

Corretude de algoritmos¶

Para ilustrar como identificar algoritmos corretos, vamos usar como exemplo um algoritmo famoso de ordenação:

insertion-sort(a) // assuma n como sendo o tamanho de a
for i = 2 to n
  elem = a[i]
  j = i − 1
  while j >= 1 and elem < a[j]
    a[j+1] = a[j]
    j = j − 1
  a[j+1] = elem

O algoritmo segue o princípio de organização de cartas de um baralho na mão de um jogador: sempre inserimos uma nova carta em sua posição correta na mão. Dessa forma, a mão sempre contém um subconjunto de cartas já ordenadas (nesse caso, usaremos inteiros para ilustrar). Para verificar a corretude do insertion-sort utilizaremos uma metodologia que lembra uma indução matemática (sendo bem sincero, É uma indução matemática adaptada ao contexto de algoritmos). Vejamos:

• Se um algoritmo não possui nenhum laço de repetição, sua corretude é de fácil verificação através da inspeção exaustiva de cada uma de suas operações, sequencialmente.
• Vamos nos concentrar, portanto, em cenários em que o algoritmo contém laços de repetição que alteram seu comportamento de acordo com o tamanho da entrada.

Para esse último caso, a técnica indutiva utilizada é denominada “invariante de loop”, e consiste da verificação de três etapas:

1. Inicialização: mostramos que alguma propriedade do algoritmo é garantida antes da entrada no loop.
2. Manutenção: mostramos que, antes de iniciar a próxima iteração do loop, a propriedade continua sendo garantida.
3. Terminação: mostramos que ao final do loop, a propriedade continua sendo garantida e que, desse fato, concluímos que o algoritmo é correto.

Naturalmente, essa dita propriedade deve ser algo relacionado ao que o algoritmo de propõe a resolver. No caso da ordenação, ordenar alguns números. Vamos aplicar a técnica para o insertion-sort. A propriedade pertinente é: “a todo momento do algoritmo, temos que alguns números já estão ordenados ($a[1 \cdots i − 1]$) e esses números são os mesmos que, originalmente, se encontravam nas mesmas posições $(1 \cdots i − 1)$”. Inicialização: antes do loop, $i = 2$, e por isso o arranjp $a[1 \cdots 1]$ está ordenado trivialmente. Manutenção: antes de iniciar uma próxima iteração, temos que $a[1 \cdots i − 1]$ é um subarranjo ordenado. Em uma iteração $i$, o algoritmo posiciona $a[i]$ em sua posição correta/ordenada em $a[1 \cdots i − 1]$ realizando o deslocamento de elementos maiores enquanto for necessário. Assim, ao final, da iteração i temos os mesmos elementos $a[1 \cdots i]$ mas ordenados. Terminação: ao final da última iteração, $i = n + 1$. Como $a[1 \cdots i − 1]$ está ordenado, então $a[1 \cdots n + 1 − 1] = a[1 \cdots n]$ também estará. Qualquer algoritmo com laços pode ser verificado formalmente utilizando invariantes e se o algo- ritmo contiver vários laços, um conjunto de invariantes pode ser usado para garantir sua corretude globalmente.

Notações assintóticas¶

Quando analisamos um algoritmo, tipicamente queremos encontrar uma função matemática que representa a complexidade de tempo ou espaço sob algumas condições (como o contexto de análise, por exemplo). Na prática, essas funções podem ser bem diversas em termos de constantes e termos. Por exemplo, $n^2/2 + n/2 − 1$ poderia ser uma função que representa o crescimento do número de operações do algoritmo à medida que o tamanho da entrada cresce ($n \to \infty$). Esse polinômio tem grau 2, apesar de todos os coeficientes e termos da função, assim como $n^2$ é outro polinômio de grau 2. O interessante é que o fato de ser um polinômio de grau 2, independentemente dos coeficientes e termos, já nos remete ao formato da curva dessa função: uma parábola. Como veremos, as notações assintóticas nos ajudam justamente a categorizar funções cujas ordens de crescimento (ou formatos de curva) são equivalentes.

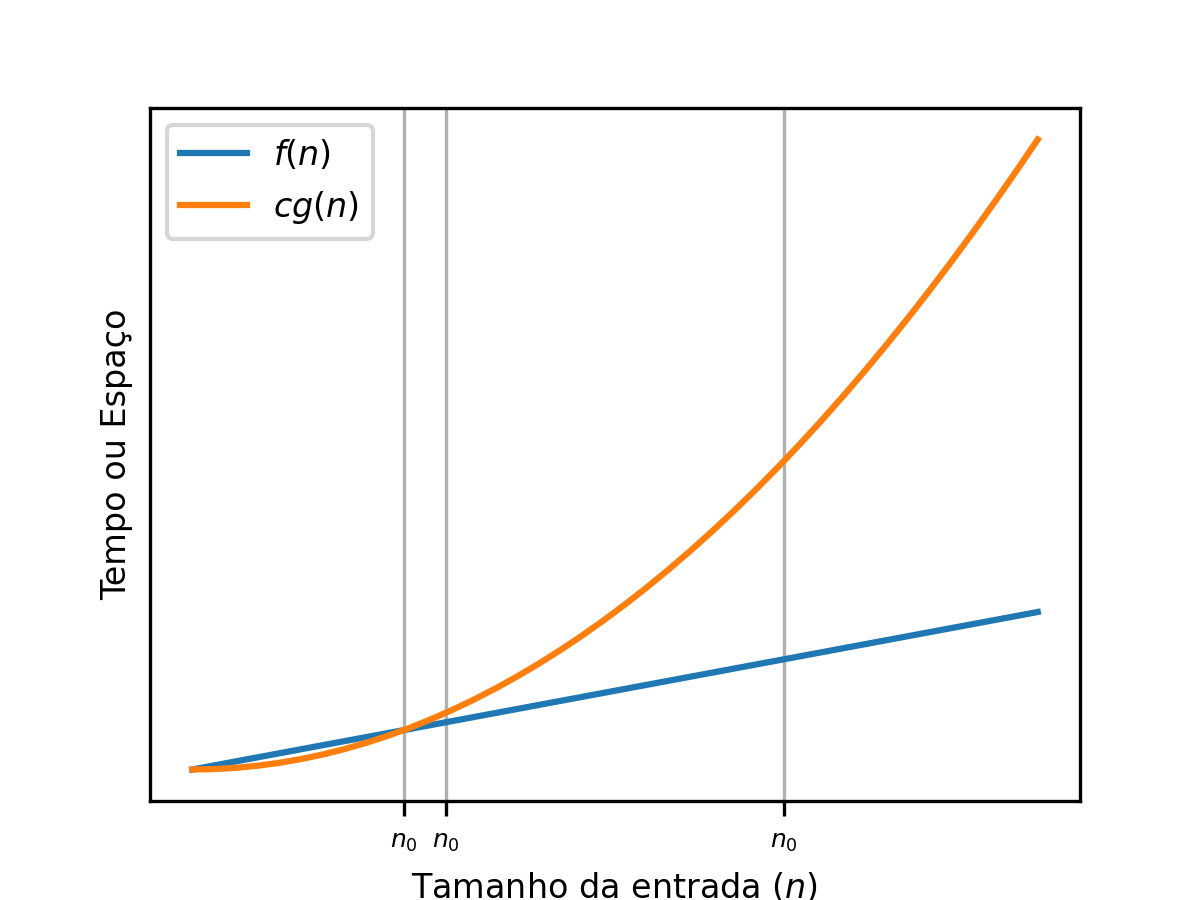
Big-Oh ou $O(g(n))$: um limite superior para o crescimento de funções¶

Esta notação é utilizada para estabelecer um limite superior para o crescimento de funções (nesse caso, $g(n)$). Dessa forma, $n^2 + n \in O(n^2)$ pois nada cresce mais do que o termo quadrático quando $n \to \infty$. Da mesma forma, $n \in O(n^2)$, já que uma parábola sempre irá ultrapassar uma reta a partir de algum momento. Formalmente, $f(n) \in O(g(n))$ sse: existirem constantes $c > 0$ e $n_0 ≥ 0$ ($c \in \mathbb{R}^+, n_0 \in \mathbb{Z}^+$) tais que: $f(n) \leq cg(n)$ para todo $n \geq n_0$.

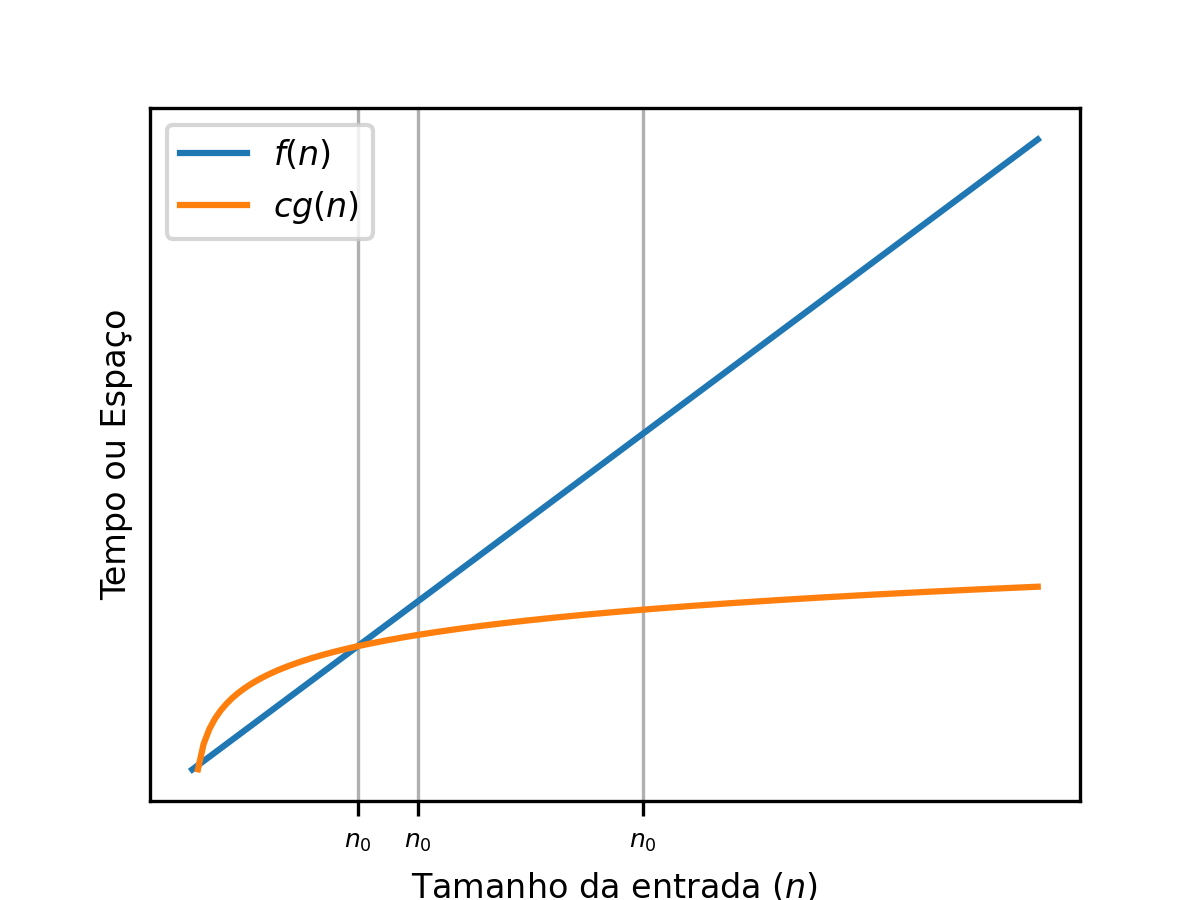
Big-Omega ou $\Omega(g(n))$: um limite inferior para o crescimento de funções¶

É utilizada para representar limites inferiores de funções. Assim, quando $n \to \infty$, $n\log n \in \Omega(n)$ e $n^2 \in \Omega(n^2)$, mas $n + 7 \notin \Omega(n^2)$. Veja a seguir uma ilustraçao que indica isso: Formalmente, $f(n) \in \Omega(g(n))$ sse: Existirem constantes $c > 0$ e $n_0 /geq 0$ ($c \in \mathbb{R}^+, n_0 \in \mathbb{Z}^+$) tais que: $f(n) \geq cg(n)$ para todo $n \geq n_0$.

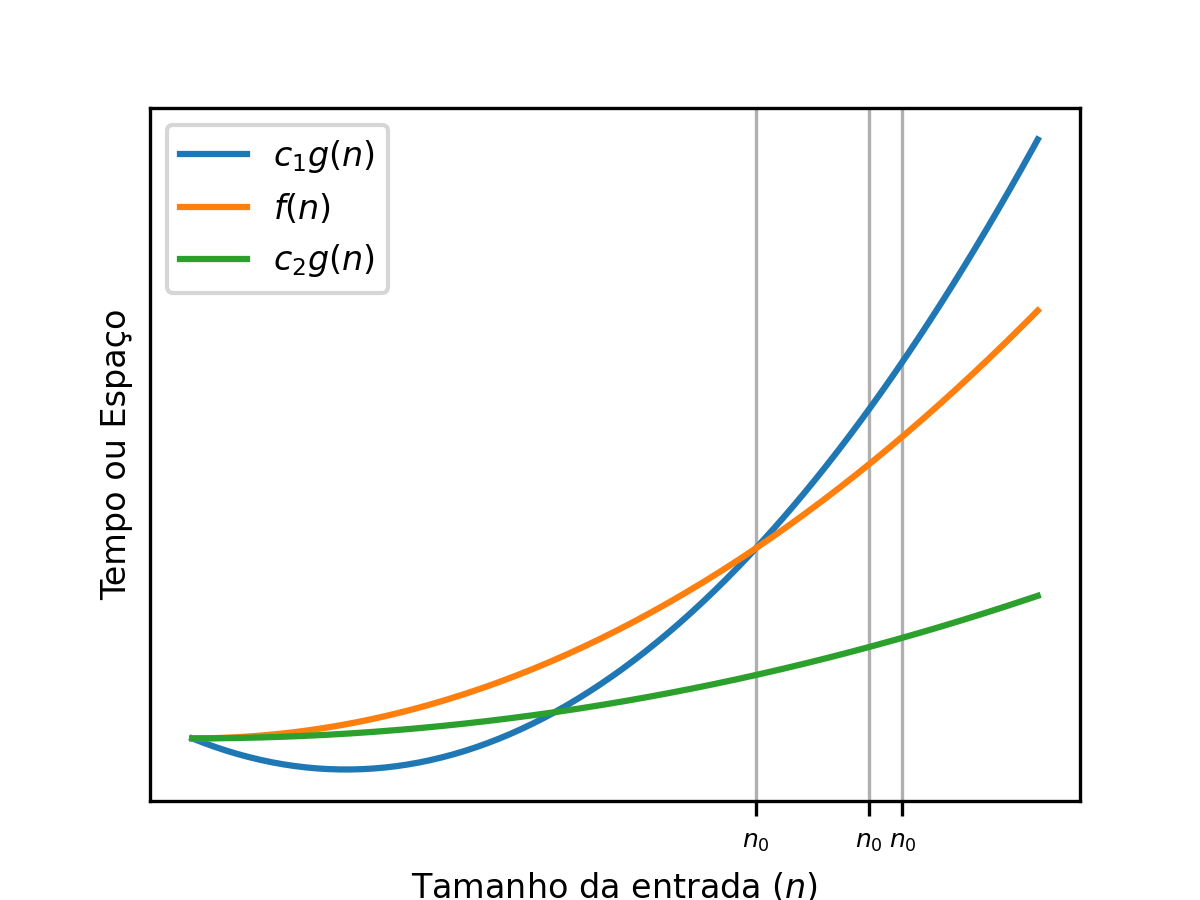
Big-Theta ou $\Theta(g(n))$: um limite justo para o crescimento de funções¶

Um limite justo é usado para representar os casos em que uma função pode ser limitada tanto inferiormente (Ω) quanto superiormente ($O$) por uma outra função. De maneira informal, dizer que $f(n) \in \Theta(g(n))$ equivale a afirmar que ambas as funções possuem exatamente a mesma ordem de crescimento assintótico. Formalmente, $f(n) \in \Theta(g(n))$ sse $f(n) \in \Omega(g(n))$ e $f(n) \in O(g(n))$.

Analisando algoritmos iterativos¶

Analisando algoritmos recursivos¶