Algoritmos de ordenação - Algoritmos: Notas e Compilações

Ordenação bolha (bubblesort)¶

A ideia do bubblesort é realizar sucessivas trocas de elementos adjacentes que estejam fora de ordem até que todos estejam garantidamente em sua posição correta ordenada. É importante observar que a quantidade máxima de vezes em que um elemento do arranjo se encontre fora de ordem com seu adjacente é $n-1$ , sendo $n$ o tamanho do arranjo. Em outras palavras, ele deveria ser trocado com todos os outros elementos do arranjo que não ele próprio e por isso, o laço mais externo do algoritmo é executado $n-1$ vezes. Na primeira iteração, o menor elemento é levado à primeira posição. Na segunda iteração, o segundo menor é levado à segunda posição, e assim por diante.

bubble-sort(a)
// argumentos:
// a: arranjo a ser ordenado, com n = |a| elementos

  n = |a|
  for i = 1 to n-1
    for j = n down to i+1
      if a[j] < a[j-1]
        swap(a, j, j-1)

Complexidade de tempo (pior caso e melhor caso): $\Theta(n^2)$ , pois a operação de comparação entre elementos acontece sem restrições dentro dos dois laços aninhados.
Complexidade de espaço (pior caso e melhor caso): $\Theta(1)$ , pois usamos apenas uma quantidade constante de memória para variáveis auxiliares além da memória fornecida na entrada.

Ordenação por inserção (insertionsort)¶

A ideia do insertion sort é começar com um subarranjo ordenado e adicionar elemento a elemento em sua posição correta no nesse subarranho ordenado. Ao final, o subarranjo ordenado vai conter todos os elementos do arranjo e portanto, o problema estará resolvido. A analogia para este método é a ordenação de cartas de baralho na mão: a cada carta retirada do monte é posicionado na ordem, em sua posição correta na sequência em construção.

insertion-sort(a)
// argumentos:
// a: arranjo a ser ordenado, com n = |a| elementos

  n = |a|
  for i = 2 to n
    elem = a[i]
    j = i - 1
    while j >= 1 and elem < a[j]
      a[j+1] = a[j]
      j = j - 1
    a[j+1] = elem

Complexidade de tempo (pior caso): $\Theta(n^2)$ , sendo que isso acontece quando a comparação elem < a[j] acontece todas as vezes possíveis a cada iteração do laço exterior, isto é, $i-1$ vezes.
Complexidade de tempo (melhor caso): $\Theta(n)$ , sendo que isso acontece quando a comparação elem < a[j] é feita apenas uma vez a cada iteração do laço exterior, isto é, quando o arranjo já se encontrar ordenado.
Complexidade de espaço (pior caso e melhor caso): $\Theta(1)$ , pois usamos apenas uma quantidade constante de memória para variáveis auxiliares além da memória fornecida na entrada.

Ordenação por intercalação (mergesort)¶

O merge sort é um algoritmo de divisão e conquista que utiliza intercalação para combinar subarranjos ordenados dois a dois em arranjos maiores também ordenados. O processo de intercalação (merge) pode ser feito de forma eficiente em tempo linear partindo da premissa que os arranjos de entrada são fornecidos ordenados.

merge(left, right, a)
// argumentos:
// left: subarranjo ordenado com n elementos
// right: subarranjo ordenado com m elementos
// a: arranjo de saída com n + m posições

  n = |left|
  m = |right|
  i = 1
  j = 1
  k = 1
  while i <= n and j <= m
    if left[i] < right[j]
      a[k] = left[i]
      i = i + 1
    else
      a[k] = right[j]
      j = j + 1
    k = k + 1
  while i <= n
    a[k] = left[i]
    i = i + 1
    k = k + 1
  while j <= m
    a[k] = right[j]
    j = j + 1
    k = k + 1

merge-sort(a)
// argumentos:
// a: arranjo a ser ordenado, com n = |a| elementos

  n = |a|
  if n == 1 or n == 0
    return
  mid = floor(n / 2)
  left = a[1, ..., mid]
  right = a[mid+1, ..., n]
  merge-sort(left)
  merge-sort(right)
  merge(left, right, a)

Complexidade de tempo (pior caso e melhor caso): A recorrência desse algoritmo é a seguinte:

$T(n) = \begin{cases} 2T(n/2) + \Theta(n) & n > 1 \\ \Theta(1) & n = 1 \end{cases}$

Pois resolvemos dois subproblemas de metade do tamanho original $n$ ( $2T(n/2)$ ), representando o custo de conquistar; gastamos $\Theta(1)$ para dividir com o problema com uma operação aritmética simples; e gastamos $\Theta(n)$ para criar os dois arranjos intermediários das metades e para intercalá-los (merge).

Complexidade de espaço (pior caso e melhor caso): $\Theta(n)$ , por conta dos dois arranjos das metades que precisam ser alocados para as chamadas recursivas.

Quicksort¶

partition(a, l, r)
// argumentos:
// a: arranjo a ser particionado, indexado de l a r, inclusive
// l: posição inicial do subarranjo
// r: posição final do subarranjo

  pivot = a[r]
  i = l - 1
  for j = l to r-1
    if a[j] <= pivot
      i = i + 1
      swap(a, j, i)    // troca elementos de posição
  swap(a, i+1, r)
  return i+1

quicksort(a, l, r)
// argumentos:
// a: arranjo a ser ordenado, indexado de l a r, inclusive
// l: posição inicial do subarranjo
// r: posição final do subarranjo

  if l >= r
    return
  p = partition(a, l, r)
  quicksort(a, l, p - 1)
  quicksort(a, p + 1, r)

Complexidade de tempo (pior caso): $\Theta(n^2)$ , representando duas partições desbalanceadas, uma com zero elementos e uma com todo o restante de elementos menos o pivot. Se isso acontecer, a cada chamada o problema diminui de apenas uma unidade (o pivot).
Complexidade de tempo (melhor caso): $\Theta(n\log n)$ , representando um particionamento ideal a cada chamada recursiva, isto é, totalmente balanceado.
Complexidade de espaço: $\Theta(1)$ , pois o algoritmo é in-place.

Heapsort¶

O algoritmo se baseia em uma estrutura de dados chamada heap, usada para garantir o acesso ao maior (ou menor) elemento com custo constante. O heap máximo pode ser visualizado como uma árvore binária de chaves que mantém a seguinte propriedade: todo nó filho da árvore é menor ou igual ao seu pai. Uma característica importante dessas estruturas heap é que se houver alguma violação de sua propriedade em um único nó, é possível reorganizar seus itens em um heap válido em tempo $\Theta(\log n)$ – isso é feito através do procedimento max-heapify.

left(i)
// argumentos:
// i: índice no heap

  return 2 * i

right(i)
// argumentos:
// i: índice no heap

  return 2 * i + 1

max-heapify(a, i)
// argumentos:
// a: heap máximo armazenado como arranjo, com tamanho a.heapsize
// i: posição do nó que pode violar a propriedade do heap

  l = left(i)
  r = right(i)
  if l <= a.heapsize and a[l] > a[i]
    largest = l
  else
    largest = i
  if r <= a.heapsize and a[r] > a[largest]
    largest = r
  if largest != i
    swap(a, largest, i)
    max-heapify(a, largest)

build-max-heap(a)
// argumentos:
// a: arranjo a ser transformado em um heap máximo

  a.heapsize = a.length
  for i = floor(a.length / 2) down to 1
    max-heapify(a, i)

heap-sort(a)
// argumentos:
// a: arranjo a ser ordenado

  build-max-heap(a)
  for i = a.heapsize down to 2
    swap(a, 1, i)
    a.heapsize = a.heapsize - 1
    max-heapify(a, 1)

Complexidade de tempo (pior caso): $\Theta(n \log n)$ . A complexidade do algoritmo max-heapify é da ordem da altura do nó na posição $i$ . O procedimento build-max-heap realiza chamadas ao max-heapify na metade dos nós (a segunda metade sempre serão folhas da árvore binária e portanto, já são heaps válidos!). Por ser uma árvore binária, temos mais nós com altura pequena do que nós com altura grande e portanto, ao somar os custos de max-heapify para cada nó na metade inferior do arranjo, temos um somatório que descresce muito rápido em seus termos, levando a um custo linear $\Theta(n)$ . Juntando tudo, o procedimento heap sort realiza $n-1$ chamadas ao procedimento max-heapify e esse custo domina a chamada inicial linear da construção do heap.
Complexidade de espaço: $\Theta(1)$ , pois o algoritmo é in-place.

Ordenação em tempo linear¶

Uma abordagem tradicional em estudo de algoritmos é classificá-los em classes de complexidade assintótica, permitindo a comparação direta entre algoritmos. Uma segunda abordagem complementar é ser capaz de afirmar algo sobre a complexidade de um problema frente a um modelo de computação. Em outras palavras, podemos querer responder o seguinte:

“Dados um modelo de computação e um problema, qual é a complexidade mínima que um algoritmo precisa ter para ser correto em solucionar o problema?”

Veja que a resposta para essa pergunta seria uma afirmação muito mais forte do que dizer algo sobre a complexidade de algoritmos isoladamente, já que ela envolve considerar todos os infinitos e possíveis algoritmos que solucionam um problema. Chamamos isso de limites inferiores para problemas.

Limite inferior para ordenação¶

Se considerarmos um modelo de computação baseado em operações de comparação, podemos ilustrar a operação de qualquer algoritmo de ordenação através de uma árvore de decisão. Uma árvore de decisão é uma árvore binária onde cada nó representa uma comparação feita em algum momento no algoritmo (operação) e as arestas representam as respostas para essas comparações: verdadeiro ou falso. Dessa forma, um caminho da raíz até uma das folhas dessa árvore representa uma execução do algoritmo, ou o conjunto de testes/decisões que o algoritmo toma dependendo da entrada. Veja um exemplo para um algoritmo que ordena três letras:

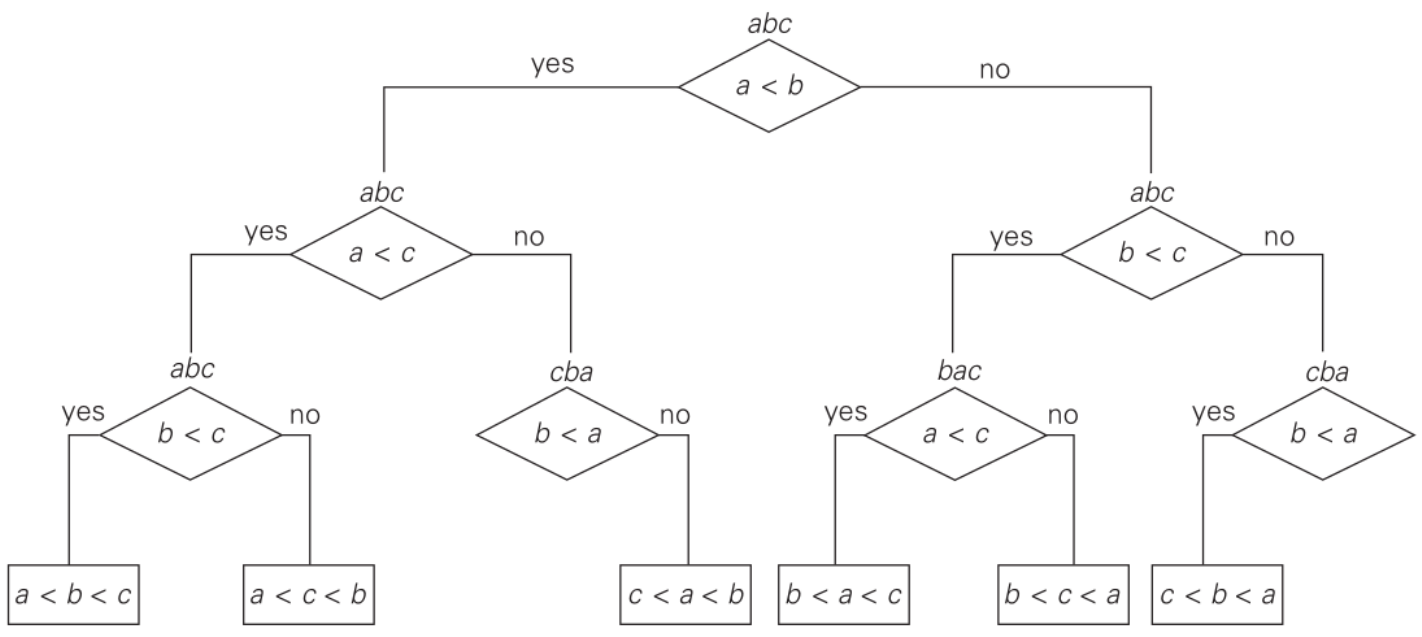
Podemos generalizar para o problema de ordenação de um arranjo qualquer $[a_1,\cdots, a_n]$ e vamos constatar que as folhas dessa árvore binária de decisão representam possíveis saídas de um algoritmo de ordenação, isto é: $\#folhas \geq n!$ , pois cada permutação do arranjo precisa ter uma folha representante, senão o algoritmo seria incorreto! A altura dessa árvore representa exatamente o número de comparações (operações) realizadas em alguma execução, seja lá qual for o algoritmo. Dessa forma, se estimarmos a altura da árvore estaremos na verdade estimando o custo mínimo que um algoritmo de ordenação precisa ter para resolver o problema corretamente para qualquer instância de entrada. Sabemos também que a altura $h$ de uma árvore binária com $k$ folhas é, pelo menos, $log_2(k)$ :

\begin{align*} \text{Sabemos que: }& h \geq \log_2(\#folhas), \#folhas \geq n! \\ \text{Aplicando log e combinando: }& h \geq \log_2(\#folhas) \geq \log_2(n!) \\ \text{Desenvolvendo: }& h \geq \log_2(n!) = \log_2(n) + \log_2(n-1) + \cdots + \log_2(1) \\ &\geq \sum_{i=1}^{n} \log_2(i) \geq \sum_{i=n/2}^{n} \log_2(i) \geq \sum_{i=n/2}^n \log_2(n/2) \\ & = \sum_{i=n/2}^n \log_2(n/2) - \sum_{i=n/2}^n \log_2(2) \\ & = (n/2 + 1)\log_2(n/2) - (n/2 + 1) \in \Omega(n\log_2 n) \end{align*}

(1)

Conclusão: Não pode existir nenhum algoritmo para o modelo de computação baseado em comparações que tenha um custo assintótico melhor do que $\Omega(n \log n)$ .

Ordenação por contagem (countingsort)¶

A primeira etapa é alocar um arranjo de tamanho $k + 1$ que será usado para contar o número de ocorrências de cada elemento. Com isso, vamos acumular nas posições de $C$ de maneira que $C[i]$ contenha o número de elementos $\leq i$ , dessa forma podemos identificar para cada elemento de $A$ a posição exata que ele deve ocupar no arranjo ordenado $B$ . Com $C$ iremos então, para cada elemento de $A$ em sua ordem inversa, colocá-lo na sua posição correta em $B$ . Toda vez que adicionamos um novo elemento em sua posição correta precisamos decrementar a quantidade de elementos menores ou iguais àquele, para que repetições de um mesmo elemento possam ser posicionadas em suas posições corretas também.

counting-sort(A, B, k)
// argumentos:
// A: arranjo de entrada com A.length elementos, com chaves inteiras em 0 ... k
// B: arranjo de saída, com as mesmas posições de A
// k: maior chave possível dos elementos de A

  C = new array with positions 0 ... k
  for i = 0 to k
    C[i] = 0
  for j = 1 to A.length
    C[A[j]] = C[A[j]] + 1
  for i = 1 to k
    C[i] = C[i] + C[i - 1]
  for j = A.length down to 1
    B[C[A[j]]] = A[j]
    C[A[j]] = C[A[j]] - 1

Radix sort¶

radix-sort(A)
// argumentos:
// A: arranjo de inteiros não negativos

  max_val = max(A)
  exp = 1
  B = new array of length |A|
  while max_val / exp > 0
    counting-sort-by-digit(A, B, 9, exp)
    copy B into A
    exp = exp * 10
  return A

counting-sort-by-digit(A, B, k, exp)
// argumentos:
// A: arranjo de entrada com A.length elementos
// B: arranjo de saída, com as mesmas posições de A
// k: maior dígito possível (9 para base 10)
// exp: posição do dígito pela qual ordenar (1, 10, 100, ...)

  C = new array with positions 0 ... k, filled with 0
  for j = 1 to A.length
    digit = (A[j] / exp) % (k + 1)
    C[digit] = C[digit] + 1
  for i = 1 to k
    C[i] = C[i] + C[i - 1]
  for j = A.length down to 1    // itera ao contrário para preservar estabilidade
    digit = (A[j] / exp) % (k + 1)
    B[C[digit]] = A[j]
    C[digit] = C[digit] - 1

Bucket sort¶

bucket-sort(A, k)
// argumentos:
// A: arranjo de n elementos com chaves não negativas
// k: número de baldes

  n = |A|
  B = new array of k empty lists    // baldes indexados de 0 ... k-1
  M = 1 + max(A)    // reescala as chaves para o intervalo [0, k)
  for i = 1 to n
    index = floor(k * A[i] / M)    // posição do balde: 0 ... k-1
    append A[i] to B[index]
  for i = 0 to k - 1
    insertion-sort(B[i])    // ou qualquer outro algoritmo de ordenação
  result = new array of length n
  j = 1
  for i = 0 to k - 1
    for each element in B[i]
      result[j] = element
      j = j + 1
  return result