Programação dinâmica

A special thanks to the TA Filipe Vilas Boas for scribing this page

Projeto de algoritmos usando Programação Dinâmica¶

Este é um paradigma de projeto de algoritmos também aplicado a problemas de otimização. Partimos da observação de que muitas vezes, o processo de decomposição de um problema em subproblemas de forma recursiva pode gerar repetidas vezes subproblemas idênticos. Esse comportamento que aparece em diversos problemas de otimização que exibem subestrutura ótima é conhecido como sobreposição de subproblemas. Portanto, essas são as características que um problema precisa exibir para que seja passível de aplicar estratégias de programação dinâmica: subestrutura ótima e sobreposição de subproblemas.

Ilustrando os princípios de programação dinâmica através de algoritmos para a sequência de Fibonacci¶

A seguinte função recursiva define o valor do n-ésimo elemento da sequência de Fibonacci:

Observe que uma definição como essa nos permite, imediatamente, definir um algoritmo recursivo para o problema:

fib(n)
   if n = 1 or n = 2
      return 1
   else
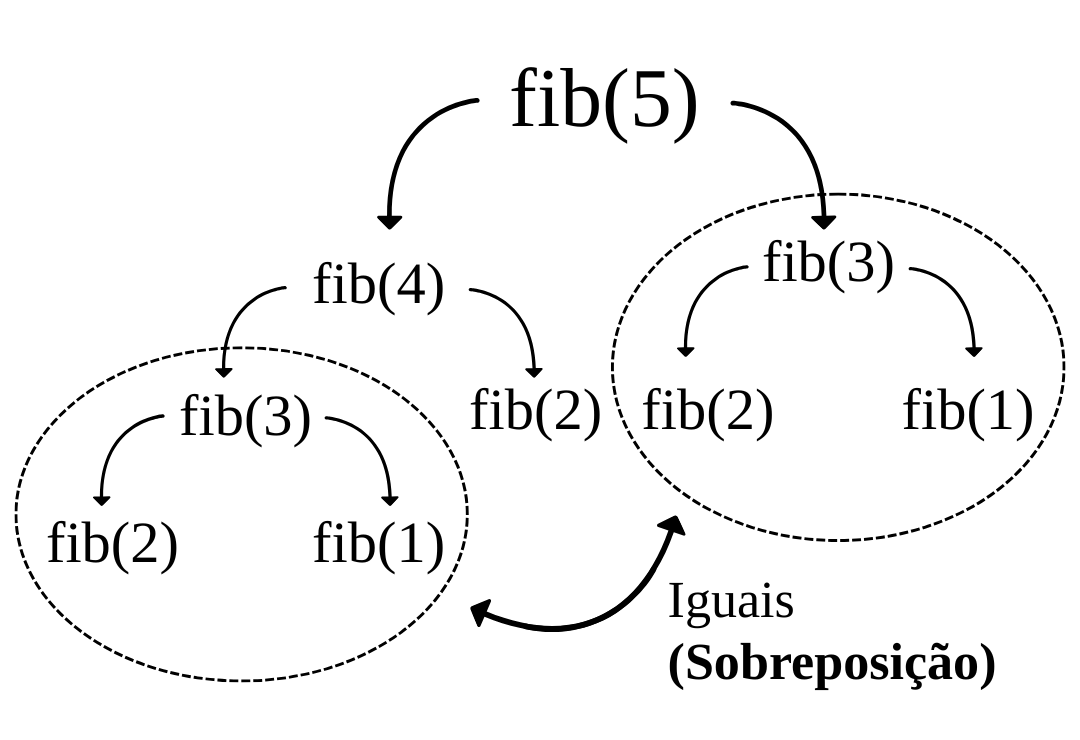
      return fib(n-1) + fib(n-2)

Ao utilizar o algoritmo acima para calcular o quinto elemento da sequência, a seguinte árvore de recursão representaria a execução do algoritmo, indicando a existência de sobreposição entre subproblemas:

Podemos analisar o algoritmo recursivo por exemplo, em relação ao número de somas. A seguinte recorrência representa esse custo em tempo:

A resolução da recorrência revela que o custo do algoritmo é exponencial. Na verdade, como a árvore de recursão para o custo dessa recorrência é desbalanceada podemos encontrar um limite inferior para o custo. Sabemos que sempre um dos ramos da árvore alcançará as folhas mais rapidamente $(T (n − 2))$ e outro demorará mais para alcançar as folhas $(T (n − 1))$. Na verdade, a diferença entre essas duas profundidades é exatamente a metade da altura total da árvore, já que um decresce de um-em-um e outro decresce de dois-em-dois (duas vezes mais rápido). Sendo assim, das profundidades 0 até $⌊n/2⌋$ com certeza a árvore permanece completa. Portanto, metade dessa árvore de custos nos dá um limite inferior para a complexidade:

A sobreposição de subproblemas nos permite “memorizar” soluções já encontradas. Veja o seguinte algoritmo modificado:

fib-memo(n)
   a[1,..., n] = [0, ..., 0]
   return fib-memo-rec(n, a)

fib-memo-rec(n, a)
   if a[n] != 0
      return a[n]
   if n = 1 or n = 2
      f = 1
   else
      f = fib(n-1) + fib(n-2)
   a[n] = f
   return f

Esse é a primeira técnica utilizada em todo algoritmo de programação dinâmica: memorização. Entretanto, nem toda memorização é um algoritmo de programação dinâmica. Para configurar um algoritmo de programação dinâmica, precisamos ter um algoritmo que memoriza soluções de subproblemas mas que ao mesmo tempo resolve os subproblemas de forma deliberada, isto é, utilizando uma ordem específica. Essa ordem sempre parte de subproblemas menores para subproblemas maiores e, portanto, dizemos que programação dinâmica é memorização feita de forma bottom-up. Para o problema estudado, temos a seguinte algoritmo com todas essas características:

fib-pd(n)
   a[1,..., n] = new array with positions 1 ... n
   a[1] = 1
   a[2] = 1
   for i = 3 to n
      a[i] = a[i-1] + a[i-2]
   return a[n]

Estudo de caso: corte de hastes¶

Entrada: Inteiros $p_1, p_2, · · · , p_n$ representando preços de corte de uma haste de tamanho $n$; Saida: preço de venda do corte ótimo.

Seja $r_n$ o preço de venda ótimo, vamos representar a equação de custos de uma solução ótima:

corte-hastes(p, n)
   if n = 0
      return 0
   melhor = -infinity
   for i from 1 to n
      melhor = max(melhor, p[i] + corte-hastes(p, n-i))
   return melhor

Estudo de caso: problema da mochila¶

Seja $c(i, j)$ o custo ótimo de uma solução para o problema da mochila que considerou até o item $i$ (0, · · · , $i$, com 0 representando que nenhum item foi considerado até então) para uma mochila de capacidade $j$:

mochila(i, j)
   if i = 0 or j = 0
      return 0
   if w[i] > j
      return mochila(i-1, j)
   else
      return max(mochila(i-1, j), v[i] + mochila(i-1, j-w[i]))

where i : 0 ... n, j : 0 ... W

Estudo de caso: máxima subsequência crescente¶

Vamos assumir que o arranjo começa de 0 e que nessa posição contém $−∞$ para indicar o último elemento de uma subsequência vazia.

Seja $c(i, j)$ o custo ótima de uma solução ótima para a subsequência $a[ j..n]$ com todos os elementos sendo maiores do que $a[i]$. Isto é, se $a[i]$ for o primeiro elemento da subsequência, podemos contatenar com esse elemento $a[i]$ uma subsequência crescente de $a[ j..n]$ desde que todos os seus elementos sejam maiores do que $a[i]$, para garantir a propriedade de estritamente crescente:

max-subseq(i, j)
   if i = 0 or j > n
      return 0
   if a[j] <= a[i]
      return max-subseq(i, j+1)
   else
      return max(max-subseq(i, j+1), 1 + max-subseq(j, j+1))

Result will be in max-subseq(0, 1): largest subsequence of a[1..n] with all elements greater than a[0] = -infinity.