Algoritmos aproximativos, heurísticas e meta-herísticas

Para problemas NP-completos, e para suas respectivas versões de otimização NP-difíceis, não se conhece algoritmo determinístico que os solucione de forma exata em tempo polinomial. Apesar disso, muitos desses problemas continuam tendo importantes aplicações reais, como em logística (PCV), escalonamento de tarefas (problema da mochila - PM), ou planejamento de infraestrutura urbana (cobertura por vértices - VCOVER). Nessas situações, como a complexidade de algoritmos exatos permite apenas a solução de instâncias muito pequenas do problema em tempo factível, pode-se recorrer a estratégias não-exatas para os problemas, desde que esse relaxamento traga vantagens do ponto de vista de tempo/complexidade. Duas abordagens são seminais desse contexto:

Algoritmos aproximativos: nesse caso não se garante que as melhores soluções serão encontradas, mas tem-se um procedimento que garante quão pior qualquer solução não-exata possa ser em relação à sua contrapartida solução exata.
Heurísticas: procedimentos que não garantem que a solução exata será retornada, mas que alguma solução não exata será retornada em tempo hábil.

Algoritmos aproximativos¶

Para problemas de otimização, onde temos uma noção da qualidade de uma solução, podemos sempre comparar o custo de uma solução ótima $S^*$ com o custo de uma solução não-ótima $S$ , esta última retornada por um procedimento que não garante a otimalidade:

Maximização: $c(S) \leq c(S^*)$ (melhor é aquilo que é maior)
Minimização: $c(S^*) \leq c(S)$ (melhor é aquilo que é menor)

Definimos o fator de aproximação de uma solução aproximada como sendo a razão que expressa quantas vezes a mesma é pior do que uma solução ótima para a mesma instância de entrada, calculada da seguinte forma:

Maximização: $\frac{c(S^*)}{c(S)}$
Minimização: $\frac{c(S)}{c(S^*)}$

Observe que a mesma ideia poderia ser aplicada a qualquer solução aproximada $S$ e sua contrapartida ótima $S^*$ . Assin, chamamos um algoritmos de $\rho$ -aproximativo se, e somente se, as soluções por ele obtidas são, no máximo, $\rho$ vezes piores do que a solução ótima para qualquer que seja a instância do problema. Assim, 1-aproximativo remete a um algoritmo ótimo, enquanto 2-aproximativo remete a um algoritmo que sempre produz soluções até 2 vezes piores do que o ótimo. Da mesma forma, $\rho$ poderia ser inclusive uma função (não constante) do tamanho da entrada $f(n)$ . O último representa um esquema de aproximação para um algoritmo, cuja qualidade e fator de aproximação depende diretamente do tamanho da entrada. Em seguida, vamos focar no cenário em que o fato de aproximação $\rho$ é uma constante.

Para mostrar que um algoritmo é aproximativo, devemos então encontrar um fator de aproximação para o algoritmo $\rho$ tal que:

Maximização: $c(S^*) \leq \rho~ c(S)$
Minimização: $c(S) \leq \rho~ c(S^*)$

Exemplo 1: cobertura por vértices¶

Neste problema, dado um grafo, o objetivo é selecionar um subconjunto mínimo dos vértices tal que todas as arestas sejam incidentes em algum vértice selecionado. Um algoritmo aproximativo para o problema, e totalmente arbitrário, seria:

vcover-aproximativo(G(V,E))
   E' = E
   C = {}
   while E' != {}
      let (u,v) be an arbitrary edge in E'
      C = set-union(C, {u,v})
      remove from E' all edges incident with u or with v
   return C

Um fator de aproximação para o algoritmo pode ser derivado a partir dos seguintes fatos:

Seja $A$ as arestas escolhidas no único laço do algoritmo. Sendo assim, os vértices escolhidos em $C$ satisfazem:

$|C|=2|A|$

Seja $S^*$ uma solução ótima. Cada aresta em $A$ precisa ser coberta por, pelo menos, um vértice em $S^*$ . Isto é, uma aresta de $A$ precisa ser coberta por um vértice de $S^*$ ou por dois vértices de $S^*$ (nunca por nenhum vértice em $S^*$ , por quê?):

$c(S^*) \geq |A|$

Juntando (1) e (2):

$c(S^*) \geq |A| \implies 2c(S^*) \geq 2|A| \implies 2c(S^*) \geq 2|A| = |C|$

Isto é:

$|C| \leq 2c(S^*)$ , e por isso, temos um fator de aproximação 2 para o algoritmo. Conclusão, vcover-aproximativo se trata de um algoritmo 2-aproximativo.

Exemplo 2: problema do caixeiro viajante com desigualdade triangular (PCV)¶

Dado um grafo ponderado com arestas representando distâncias entre cidades, queremos encontrar um percurso fechado (ciclo hamiltoniano) de custo mínimo.

Uma observação interessante sobre o PCV é que deve-se passar por cada um dos vértices do grafo uma única vez, assim como no problema da árvore geradora mínima (AGM). De fato, com um ciclo hamiltoniano, podemos obter rapidamente uma árvore geradora (não necessariamente mínima):

**TODO: incluir figura

A ideia do algoritmo aproximado apresentado a seguir, busca tomar a direção inversa: encontrar um ciclo hamiltoniano a partir de uma árvore geradora. Faz sentido, já que encontrar uma árvore geradora mínima em um grafo é um problema conhecidamente fácil de se resolver e podemos contar com algoritmos polinomiais como o de Prim ou o de Kruskal. Pela dinâmica a seguir apresentada, e para que o fator de aproximação do algoritmo seja válido, vamos assumir que as instâncias do PCV atendem a propriedade da desigualdade triangular para os pesos das arestas, isto é:

$c(u,v) \leq c(u,w) + c(w,v)$ para $u,v,w \in V$

Seria o equivalente a garantir que o caminho direto entre dois vértices nunca pode ser maior do que o caminho indireto entre dois vértices. Se os pesos representarem distâncias euclidianas, por exemplo, essa propriedade é naturalmente satisfeita.

Sendo assim, dada uma AGM do grafo, como transformá-la em um ciclo hamiltoniano? Uma alternativa é possível a partir de um caminhamento em profundidade (DFS) na AGM.

*** TODO: incluir exemplo e explicação do exemplo*

pcv-aprox-agm(G(V, E))
   T* = "alguma AGM de G" // usando o Prim ou Kruskal, por exemplo
   C = "faça um caminhamento em profundidade (DFS) em T, anotando os vértices na ida
   e na volta do percurso"
   S = "elimine as repetições de vértices em C, exceto o primeiro e o último"
   retorne S

O algoritmo acima é polinomial no tamanho do grafo (verifique isso detalhando como cada linha do algoritmo alto nível acima seria implementada). A sequência de observações a seguir demonstra um fator de aproximação para o algoritmo:

Sabemos que o custo de uma solução ótima $S^*$ para o PCV é maior ou igual ao custo de uma árvore geradora qualquer $T$ , que por sua vez é maior do que o custo de uma AGM $T^*$ :

$c(S^*) \geq c(T) \geq c(T^*) \implies c(S^*) \geq c(T^*)$ -- (I)

O custo do caminhamento DFS em $T^*$ no algoritmo é $2c(T^*)$ , já que passamos duas vezes por cada aresta: na ida e na volta. Assim:

$c(C)=2c(T^*)$ -- (II)

Mas também sabemos que o custo da solução retornada pelo algoritmo, $c(S)$ , não é maior do que o caminhamento DFS de custo $2c(T^*)$ , já que o primeiro foi obtido através da remoção de vértices (e arestas) do segundo.

$c(C) \geq c(S)$ -- (III)

Então, usando os fatos anteriores:

$c(S^*) \geq_{\texttt{(I)}} c(T^*) \implies 2c(S^*) \geq 2c(T^*) =_{\texttt{(II)}} c(C) \geq_{\texttt{(III)}} c(S)$

Dessa forma, temos nosso fator de aproximação para este problema de minimização: $\rho = 2$ . Em outras palavras, os ciclos hamiltonianos retornados pelo algoritmo aproximativo são, no máximo, duas vezes piores do que a solução ótima, para qualquer que seja a instância de entrada! O algoritmo é 2-aproximativo desde que a entrada respeite a desigualdade triangular.

Exemplo de heurística gulosa: PCV - vizinho mais próximo¶

Uma heurística bastante conhecida para o problema do caixeiro viajante é a do vizinho mais próximo (nearest neighbor). Ela constrói uma solução de forma iterativa, sempre escolhendo a próxima cidade mais próxima ainda não visitada.

A heurística não garante fator de aproximação, mas é simples e eficiente para instâncias grandes.

pcv-guloso-vizinho-mais-proximo(G(V, E), v_inicial)
   S = [v_inicial]
   v = v_inicial
   enquanto |S| < |V|
      u = vértice mais próximo de v que não está em S
      S.adicione(u)
      v = u
   S.adicione(v_inicial) // fecha o ciclo
   retorne S

S é a sequência de vértices visitados (o ciclo).
Em cada passo, escolhe-se o vértice mais próximo ainda não visitado.
Ao final, retorna-se ao vértice inicial para fechar o ciclo.

Essa heurística é rápida (complexidade $O(n^2)$ para $n$ vértices), mas pode produzir soluções bem distantes do ótimo em alguns casos.

Capítulo 7 (rascunho)¶

Técnicas para tratar problemas NP-Completos¶

Começa definindo os termos
Heurísticas construtivas: funções gulosas e exemplos mochila, PCV, bin packing. Neste ponto, existe o conceito de escolher o item que mais melhora o custo a todo momento e para o problema do bin packing, temos o conceito de maximizar a utilização dos recursos.
Os slides e pseudocodigos do Thiago Noronha parecem mais simples de descrever do que os slides da referência que eu achei.
Bin packing / first fit: árvore de torneios para fazer em $O(n \;log \;n)$
Outro princípio: inserir elementos mais difíceis primeiro usando first fit decreasing
Heurísticas são mais específicas e seus princípios diferem de problema para problema, apesar de existirem similaridades. Metaheurísticas, por outro lado, se referem a estratégias mais genéricas que podem ser aplicadas diretamente a qualquer problema.
Algumas diferenciações de metaheurísticas: (1) memória: as soluções parciais podem ser armazenadas e classificadas de acordo com a qualidade delas, isso vai permitir um mecanismo de aprendizagem; (2) intensificação: soluções parecidas tendem a ter custos parecidos e podemos sempre intensificar o que de melhor achamos até o momento – exploitation; (3) diversificação: é importante que a execução seja capaz de explorar novos caminhos para que o conjunto de soluções não fiquem enviesadas apenas a um subconjunto de soluções, é preciso haver um equilíbrio – exploration.
Características de metaheurísticas: simplicidade, generalidade, eficácia (soluções quase ótimas), eficiência (quão rápido as soluções são obtidas), robustez (variância pequena entre execuções repetidas – no caso de operações não determinísticas)

7.1 Algoritmos aproximativos¶

7.1.1 Algoritmo aproximativo para o PCV com desigualdade triangular¶

[ \boxed{ \begin{array}{ll} \textbf{PCV-APROXIMATIVO-AGM}(G = (V, E)) \ 1.\quad T* \gets \text{“alguma AGM de }G ; \small{\langle \langle \text{Alg. Prim ou Kruskal} \rangle \rangle} \ 2.\quad C \gets \text{“DFS em \textit{T*}, anotando os vértices na ida e na volta do percurso”} \ 3.\quad S \gets \text{“elimine repetições de vértices em C, exceto o primeiro e o último”} \ 4.\quad \text{retorne } S \ \end{array} } ]

Sabemos que o custo de uma solução ótima S* para o PCV é maior ou igual ao custo de uma árvore geradora qualquer T , que por sua vez é maior do que o custo de uma AGM T*:

c(S^*) ≥ c(T ) ≥ c(T^*) ⇒ c(S^*) ≥ c(T^*)

(1)

O custo do caminhamento DFS em T* no algoritmo é 2c(T*), já que passamos duas vezes por cada aresta: na ida e na volta. Assim:

c(S^*) ≥ c(T^*) ⇒ 2c(S^*) ≥ 2c(T^*)

(2)

Mas também sabemos que o custo da solução retornada pelo algoritmo, c(S), não é maior do que o caminhamento DFS de custo 2c(T*), já que o primeiro foi obtido através da remoção de vértices (e arestas) do segundo. Então, por esse motivo e considerando a desigualdade triangular:

2c(S^*) ≥ 2c(T^*) ≥ c(S) ⇒ c(S) ≤ 2c(S^*)

(3)

Dessa forma, temos nosso fator de aproximação para este problema de minimização: ρ = 2. Em outras palavras, os ciclos hamiltonianos retornados pelo algoritmo aproximativo são, no máximo, 2 × piores do que a solução ótima, para qualquer que seja a instância de entrada!

7.2 Heurísticas construtivas¶

Apesar de existirem diversas divergências de nomenclatura, podemos considerar que algoritmo é um procedimento que resolve um problema de forma exata. Por outro lado, uma heurística é um procedimento que não resolve um problema sempre de forma exata mas que é projetada com o objetivo de chegar o mais próximo do exato.

Uma heurística construtiva são aqueles procedimentos que constroem passo-a-passo uma solução viável para um problema de otimização. Muitas vezes essas heurísticas construtivas são de complexidade polinomial (senão compensava mais resolver o problema de forma exata) e utilizam o paradigma de algoritmos gulosos em seu projeto. Uma heurística construtiva é, portanto, muito dependente do problema em questão e das características que temos nos elementos que compõem a solução.

7.3 Metaheurísticas¶

Uma metaheurística pode ser definida como uma metologia que guia o projeto de heurísticas para um determinado problema. Por esse motivo, metaheurísticas tem uma característica principal que é a de ser mais generalizável e aplicável a diferentes problemas de otimização. Já que o alvo desse tipo de estratégia são aqueles problemas para os quais não se conhece algoritmo polinomial determinístico para obter a solução exata, metaheurísticas trabalham no intuito de amostrar o espaço de busca de soluções de maneira a selecionar o que de melhor foi encontrado dada restrições de recursos computacionais. Três mecanismos são fundamentais:

Intensificação (exploitation) se refere à capacidade da metaheurística em melhorar (intensificar) soluções encontradas: soluções parecidas tendem a ter custos parecidos.
Diversificação (exploration) se refere à capacidade da metaheurística em diversificar o conjunto de soluções amostradas do espaço de busca, de maneira a aumentar a confiança de que o melhor encontrado de fato está razoavelmente próximo da solução ótima.
Memória se refere à capacidade da metaheurística de armazenar e classificar soluções de acordo com suas qualidades com o objetivo de aprender durante a execução quais decisões possuem maior potencial de produzir melhores resultados.

7.4 Busca em vizinhança¶

Podemos modelar o espaço de busca das soluções de um problema como um grafo (direcionado ou não): vértices representam soluções e arestas representam soluções vizinhas, isto é, soluções que puderam ser transformadas em outras a partir de algum critério (função) de transformação. Funções de vizinhança são específicas de cada problema, alguns exemplos são:

2-opt pode ser usado em problemas cuja solução pode ser representada como uma permutação de itens (vértices no PCV, por exemplo) e consiste em trocar pares de elementos da solução. Todas as maneiras diferentes de se trocar dois elementos da solução corrente, portanto, induzem às soluções vizinhas.

reinsert outra vizinhança comum para permutações consistem em reinserir cada item em todas as posições diferentes da permutação original, gerando uma vizinhança mais densa.

swap se a solução for representada por vários subconjuntos de itens, podemos considerar escolher um item de um dos subconjuntos e consider trocá-lo com outros elementos de subconjuntos diferentes. Por exemplo, problema do empacotamento.

vizinhança n¹ utilizado quando a solução pode ser representada como uma sequência de bits e consiste em considerar como vizinhas aquelas soluções que diferem de, exatamente, um bit.

Considerando o grafo implícito de soluções e a função de vizinhança, podemos delimitar duas estratégias padrão:

Em uma busca aleatória na vizinhança, a heurística salta de solução em solução aleatoriamente, sempre mantendo o que de melhor for encontrado. Conhecida como heurística do passeio aleatório (random walk).
Em uma busca local na vizinhança, a heurística salta para soluções sempre aprimorantes, até que um ótimo local seja encontrado e nenhuma solução vizinha é melhor do que a corrente.

Temos duas abordagens para realizar a busca local: (1) saltar sempre para a melhor solução aprimorante; (2) saltar sempre para a primeira solução aprimorante. A primeira abordagem tende a alcançar o ótimo local mais rapidamente, mas ao custo potencialmente elevado de gerar todos os vizinhos de uma solução a cada salto. Por outro lado, a segunda abordagem custa menos para cada salto mas tende a alcançar o ótimo local com mais passos.

Alguns problemas de se realizar busca local isoladamente:

Ótimo local pode ser muito distante do ótimo global;
A solução inicial pode influenciar muito na qualidade do ótimo local encontrado;
A vizinhança pode impactar na busca local, tanto do ponto de vista de complexidade como de qualidade;
Pode ser exponencial no pior caso: por exemplo, com apenas um ótimo local sendo o ótimo global juntamente com uma função de vizinhança que aprimora pouco a solução.

Por todos esses motivos, existem metaheurísticas baseadas em busca local que tentam fugir desses ótimos locais para encontrar soluções mais diversificadas.

7.5 Metaheurísticas baseadas em busca local: Variable Neighborhood Search¶

A ideia principal é que, para escapar de ótimos locais, podemos utilizar várias vizinhanças de forma sistemática. Uma solução pode ser um ótimo local para uma vizinhança mas não o ser para outra e portanto, temos maior chance de continuar aprimorando as soluções, mesmo que elas representem um ótimo local para alguma(s) vizinhança.

Utiliza um método conhecido como Variable Neighborhood Decent para refinar soluções utilizando várias funções de vizinhança. Chamamos de VND uma versão de VNS na qual a escolha das vizinhanças é feita de forma determinística (e não estocástica). Esse VNS baseado em VND utiliza o procedimento a seguir para aprimorar uma solução s até que uma condição de parada seja alcançada: por exemplo, tempo de relógio em um processador, número de iterações, etc.

[ \boxed{ \begin{array}{ll} \textbf{VND}(f,N_1 ... N_k, s) \ 1.\quad i \gets 1 \ 2.\quad \text{while } i ≤ k \ 3.\quad \quad s’ \gets \text{melhor vizinho em } Ni(s) \ 4.\quad \text{if } f(s’) \text{é melhor do que } f(s)\ 5.\quad \quad s \gets s’ \ 6.\quad \quad i \gets 1 \ 7.\quad \text{else} \ 8.\quad \quad i \gets i+1 \ 1.\quad \text{return } s \end{array} } ]

Outras versões de VNS que não são determinísticas existem. Nesses casos, a uma solução é aleatoriamente selecionada da vizinhança corrente (ao contrário de ser um procedimento determinístico descent) e o procedimento continua normalmente.

7.6 Metaheurísticas baseadas em busca local: GRASP¶

Se trata de uma heurística de multi-partida onde depois de encontrar um ótimo local, reinicia a busca a partir de outra solução inicial para tentar obter soluções potencialmente diferentes. O termo é uma sigla para: Greedy Randomized Adaptive Search Procedure.

O GRASP é composto de várias iterações e cada uma contendo duas fases: (1) fase construtiva, onde alguma solução inicial é gerada de forma aleatória e gulosa; (2) fase de busca local onde soluções vizinhas aprimorantes são visitadas até que o ótimo local seja alcançado. Naturalmente, o diferencial do GRASP está na fase (1).

Para conseguir fazer (1), o GRASP considera que alguma solução viável é composta de um conjunto de itens – isso é sempre verdade para algoritmos gulosos. A cada passo da construção desse conjunto solução, consideramos escolher o melhor item candidato dentre um subconjunto de todos os possíveis. Portanto, se escolhemos o melhor item dentre todos os possíveis, temos um algoritmo guloso puro; se escolhemos o melhor item dentre um subconjunto de itens, introduzimos uma certa aleatoriedade na escolha da solução inicial. Veja que esse espectro de decisão representa o compromisso do GRASP entre intensificação e diversidade, sendo controlado por um parâmetro $a$ . Considerando um problema de minimização, a lista de itens considerados no sorteio aleatório da construção da solução inicial é o seguinte, selecionamos todo item $e$ cujo custo de sua inclusão seja $c(e)$ :

c(e) ≤ c_{min} + a(c_{max} − c_{min}) \\ c_{min} \text { representa o custo do item que tem o menor custo} \\ c_{max} \text { representa o custo do item que tem o maior custo} \\

(4)

[ \boxed{ \begin{array}{ll} \textbf{SOLUCAO-INICIAL-GRASP}(\alpha) \ 1.\quad s \gets \emptyset \ 2.\quad \text{enquanto } s \text{ não for uma solução completa} \ 3.\quad \quad G \gets \text{“lista de itens candidatos”} \ 4.\quad \quad \text{avalie custos incrementais da solução para cada } g \in G \ 5.\quad \quad c_{\min} \gets \min(G) \ 6.\quad \quad c_{\max} \gets \max(G) \ 7.\quad \quad G’ \gets { g \in G \mid c(e) \leq c_{\min} + \alpha (c_{\max} - c_{\min}) } ; \small{\langle \langle \text{lista restrita de candidatos} \rangle \rangle} \ 8.\quad \quad e \gets \text{“item aleatório em } G’ \text{”} \ 9.\quad \quad \text{se } s \cup {e} \text{ for inviável} \ 10.\quad \quad \quad \text{se } s \text{ não puder se tornar viável, interrompa laço} \ 11.\quad \text{retorne } s \ \end{array} } ]

[ \boxed{ \begin{array}{ll} \textbf{GRASP}(\alpha) \ 1 \quad \text{seja } s \text{ a melhor solução encontrada} \ 2 \quad \text{enquanto condição de parada não for atingida} \ 3 \quad \quad s_0 \leftarrow \text{\footnotesize SOLUCAO-INICIAL-GRASP}(\alpha) \ 4 \quad \quad s’ \leftarrow \text{\footnotesize BUSCA-LOCAL}(s_0) \ 5 \quad \quad \text{se } s’ \text{ for melhor do que } s \ 6 \quad \quad \quad s \leftarrow s’ \ 7 \quad \text{retorne } s \ \end{array} } ]

Como podemos ver, a característica de ser guloso é dada pela seleção de itens de baixo custo na lista restrita. A característica aleatorizada é dada pela escolha aleatória de um item da lista restrita. A característica adaptativa é dada pelo cálculo da cardinalidade da lista e controlada pelo parâmetro α, deixando a estratégia independente de valores absolutos de custo.

Existem estratégias que configuram o α de maneira automática e de forma reativa. Nesse caso, podemos definir uma lista inicial de possíveis valores αi e a cada iteração escolhemos um desses valores de forma aleatória para guiar o GRASP. Inicialmente, consideramos todos os αi com a mesma probabilidade de escolha, mas toda vez que terminamos uma iteração atualizamos a chance de cada αi ser escolhido ao favorecer valores que geraram soluções melhores. A ideia é, portanto, que α convirja para αi que na média produz as melhores soluções para o problema.

7.7 Metaheurísticas baseadas em busca local: Busca Tabu¶

O princípio da busca tabu é: quando um ótimo local for alcançado numa busca local, continue realizando busca local. De certa forma, se trata de um mecanismo de tentar escapar de ótimos locais e não sofrer de convergência precoce. Naturalmente, ao se fazer isso estaremos sujeitos a revisitar soluções já visitadas no passado e pior: o algoritmo de busca pode inclusive entrar em ciclos intermináveis. Por isso, a busca tabu precisa contar com uma chamada lista tabu que armazena uma certa quantidade constante de soluções visitadas, já que não é praticável na maioria das vezes armazenar todas as soluções. Com essa informação, a busca local pode evitar sempre pular para soluções que já tenham sido visitadas.

1 Lista tabu. Se trata de um mecanismo de memória de curto prazo. Se armazenamos na lista tabu k soluções, então somos capazes de evitar ciclos de tamanho ≤ k.

2 Intensificação. Utiliza a memória de médio prazo para indentificar soluções elite e enviesar a busca na direção dessas melhores soluções.

3 Diversificação. Utiliza a memória de longo prazo para enviesar a busca no sentido oposto das soluções já amostradas – faz o inverso da intensificação ao modificar os pesos dos itens considerados para uma solução vizinha.

[ \boxed{ \begin{array}{l} \textbf{BUSCA-TABU}() \ 1 \quad s \leftarrow \text{“solução inicial”} \ 2 \quad \text{inicialize a lista tabu e as memórias de médio e longo prazos} \ 3 \quad \text{enquanto condição de parada não for atingida} \ 4 \quad \quad s’ \leftarrow \text{“solução vizinha de } s \text{ que não é tabu e que atenda aos mecanismos de aspiração”} \ 5 \quad \quad s \leftarrow s’ \ 6 \quad \quad \text{atualize a lista tabu e outros mecanismos de memória} \ 7 \quad \quad \text{aplique intensificação e/ou diversificação se necessário} \ 8 \quad \text{retorne } s \ \end{array} } ]

7.7.1 Implementação da lista tabu¶

Existem várias possíveis implementações para uma lista tabu. As menos usadas são aquelas que consideram armazenar todas as soluções encontradas, quantidade que comumente é exponencial. Outra forma utilizada é através de árvores de prefixo, que são capazes de comprimir o conjunto de soluções encontradas. Entretanto, a estratégia mais utilizada é utilizar algum mecanismo de hashing para rapidamente identificar soluções que foram encontradas.

7.8 Metaheurísticas populacionais¶

Diferentemente de metaheurísticas de busca local, estratégias populacionais trabalham iterativamente com conjuntos de soluções (populações). Dessa forma, um conjunto de soluções é substituído por outro a toda iteração, potencialmente com soluções (indivíduos) mais diversificados e/ou intensificados. Dois tipos são principais: aqueles baseados em evolução, como nos algoritmos genéticos, e aqueles baseados em memória compartilhada, como na otimização baseada em colônia de formigas.

7.9 Metaheurísticas baseadas em populações: algoritmos genéticos¶

São estratégias inspiradas na evolução por seleção natural.

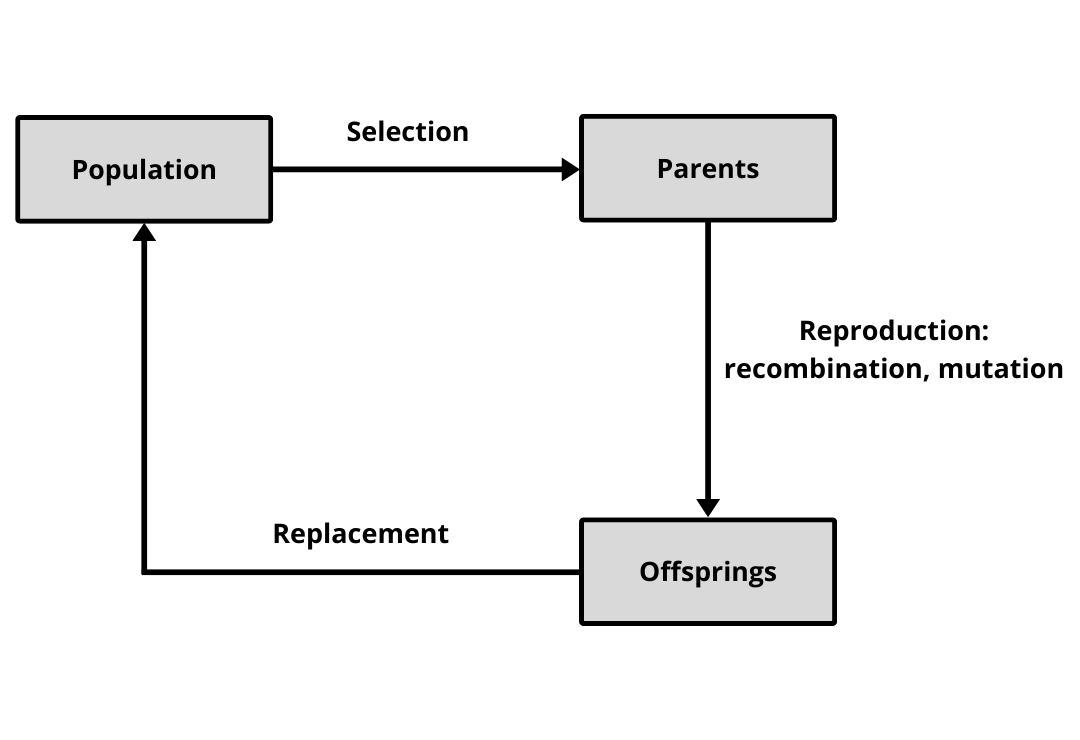
1 Seleção. Nesta etapa alguns indivíduos mais aptos serão escolhidos para se reproduzirem, isto é, soluções do conjunto serão escolhidas. Existem diversas formas para se implementar essa etapa, duas mais comuns são: sorteio por roleta e torneio. No sorteio por roleta, vamos atribuir certa probabilidade a cada solução de ser escolhida e aqui podemos utilizar diversos mecanismos de intensificação e/ou diversificação. No torneio, algumas soluções são escolhidas de forma aleatória para participarem de um torneio, por exemplo, ganhando aquela que for a melhor. Independente da forma usada para selecionar soluções do conjunto corrente, teremos um subconjunto pronto para a etapa de reprodução, na qual novas soluções derivadas das seleções serão geradas.

2 Reprodução por recombinação (intensificação). Duas ou mais soluções são combinadas em novas soluções. As soluções resultantes devem conter apenas caracteríticas presentes nos pais e por isso, qualidade não é garantida apenas a viabilidade.

3 Reprodução por mutação (diversifiação). Aqui pequenas modificações são realizadas nas soluções de forma aleatória. Uma maneira comum é considerar a vizinhança da solução e sortear um vizinho de forma aleatória.

4 Substituição. Com os novos indivíduos obtidos durante a reprodução, um novo conjunto de soluções. Podemos substituir todo o conjunto, substituir um dos pais que seja pior (estável), ou mesmo selecionar sempre as melhores soluções dentre pais e filhos (elitista).

[ \boxed{ \begin{array}{l} \textbf{ALGORITMO-GENÉTICO}() \ 1 \quad \text{gere um conjunto inicial } S \ 2 \quad \text{enquanto condição de parada não atingida} \ 3 \quad \quad P \leftarrow \text{algumas soluções para reprodução em } S ; (\text{seleção}) \ 4 \quad \quad S’ \leftarrow \text{soluções recombinadas em } P ; (\text{reprodução}) \ 5 \quad \quad S’ \leftarrow \text{soluções em } S’ \text{ com mutações } (\text{reprodução}) \ 6 \quad \quad S \leftarrow \text{soluções escolhidas em } S \cup S’ ; (\text{substituição}) \ 7 \quad \text{retorne melhor solução em } S \ \end{array} } ]

7.10 Metaheurísticas baseadas em populações: colônia de formigas¶

[ \boxed{ \begin{array}{l} \textbf{COLONIA-FORMIGAS}(\alpha, \beta, \rho, \delta, n) \ 1 \quad \text{seja } S \text{ um conjunto de soluções (população)} \ 2 \quad \text{inicialize a memória adaptativa } \tau_e \text{ para cada item } e \ 3 \quad p \leftarrow \text{\footnotesize CALCULA-PROBABILIDADES-ITENS}(\tau, n, \alpha, \beta) \ 4 \quad \text{enquanto condição de parada não atingida} \ 5 \quad \quad S \leftarrow \text{\footnotesize CONSTROI-SOLUCOES}(p) \ 6 \quad \quad \tau \leftarrow \text{\footnotesize ATUALIZA-MEMORIA}(\tau, \rho, \delta) \ 7 \quad \quad p \leftarrow \text{\footnotesize CALCULA-PROBABILIDADES-ITENS}(\tau, n, \alpha, \beta) \ 8 \quad \text{retorne melhor solução em } S \ \end{array} } ]

Algoritmos: Notas e Compilações

Teoria da Complexidade de Algoritmos

Algoritmos: Notas e Compilações

Algoritmos aproximativos [LAB-1]